算法 - 后缀自动机 & 回文自动机
写这篇文章的用意主要是记录一下我曾经学会过 SAM。
后缀自动机
主要学习资料
http://wyfcyx.is-programmer.com/posts/76107.html (对我的帮助最大)
http://www.cnblogs.com/Robert-Yuan/p/5187439.html (相当详细)
2012年noi冬令营陈立杰讲稿.ppt (始祖)
https://chrt.github.io/2017/04/21/suffix-automaton/ (看到这个我觉得我不用再写这篇文章了)
https://zhuanlan.zhihu.com/p/25948077 (复杂度“证明”)
SAM 是一种确定有限状态自动机 (DFA),它能够接受所有字符串的所有后缀。
重要的信息有 tranc(x, c) 和 fa(x),有两种理解方式:
- 自动机形态
- tranc(x, c) 为状态 x 接受字符 c 后到达的状态
- fa(x) 是 right(x) 的超集中最小的所对应的状态
- 后缀树形态(逆序)
- fa(x) 是 x 的父节点
- tranc(x, c) 是 x 对应的后缀在首部增加字符 c 后所形成的后缀在树中对应的结点
- 自动机形态
无论那种理解方式,反正可以互相转换。鉴于后缀树更为直观、简洁,那么就以这种方式来描述。
对于一个字符串 s(|s| = n),建立它的后缀 trie,就形成了它的后缀树,但这样效率和空间都很糟糕。如果对 trie 中的单链进行压缩,那么可以证明,结点个数是 O(n) 的。(证明:借用虚树复杂的证明,n 个叶节点都是关键点,而关键点两两之间的 LCA 不超过 n − 1,所以总的结点数不超过 2n − 1 个。)
接下来的关键是如何在线性时间内构造一棵压缩后的后缀树。
先给张图,未完待续。
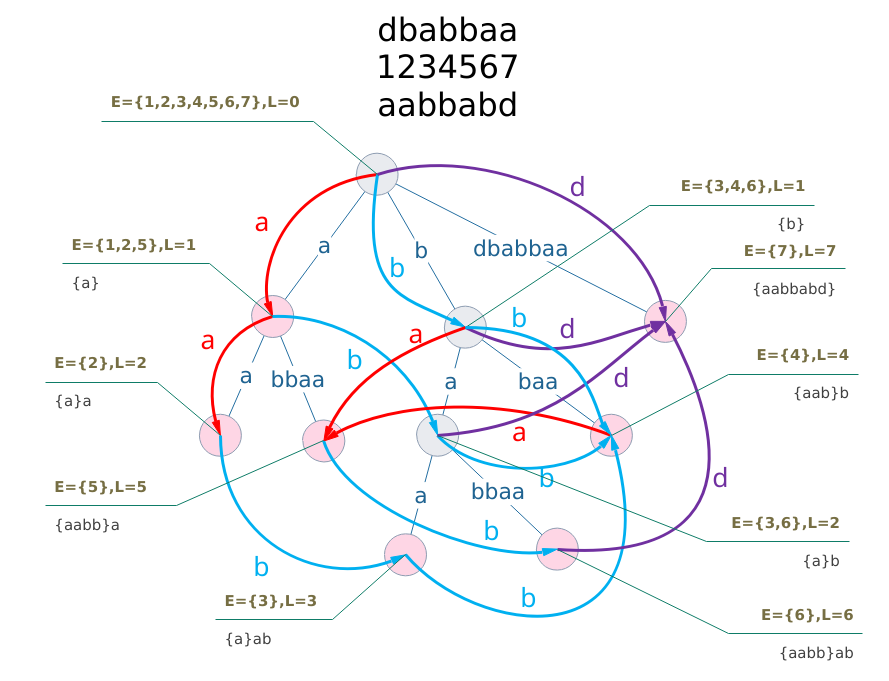
一些性质
fa 指针组成的是反串的后缀树,当然是树了。tranc 指针组成的是 DFA,所以是一个有向无环图(DAG),存在拓扑序。
tranc 指针使 len 增加,fa 指针使 len 减少。
关键点(红色标记)自带一个 EndPos,然后每个结点的 EndPos 集合是自己和子节点的 EndPos 集合的并集,且子节点以及本身的 EndPos 集合之间没有交集。
接受状态是 last 状态到根的链上的所有状态。
len 的大小是父节点的 len 加上父边压缩的字符数。
[lenmin, lenmax] 的区间大小是由 tranc 转移过来的状态的区间大小之和。
一些套路
- 如果要快速找到一个子串对应的状态,可以在后缀树上倍增。比如要找 [l, r] 的子串,那么找到 [1, r] 逆序的所在的关键点,然后往上爬 l - 1 个长度。
- cnt 表示该状态的 EndPos 集合的大小,可以在建完自动机后累加得到。
- 如果要进行多串匹配的话,不妨使用广义后缀自动机,往往会简单一些。
- 如果可以离线,可以用树上启发式合并得到每个点的 EndPos 集合。
- 如果要维护 EndPos 相关的信息,来一发 LCT。
- 获取拓扑序可以按照 len 进行基数排序。
- 为了某个状态具体的字符串内容,可以记录 EndPos 中的某一个元素。
回文自动机
相比后缀自动机,还是简单不少的。
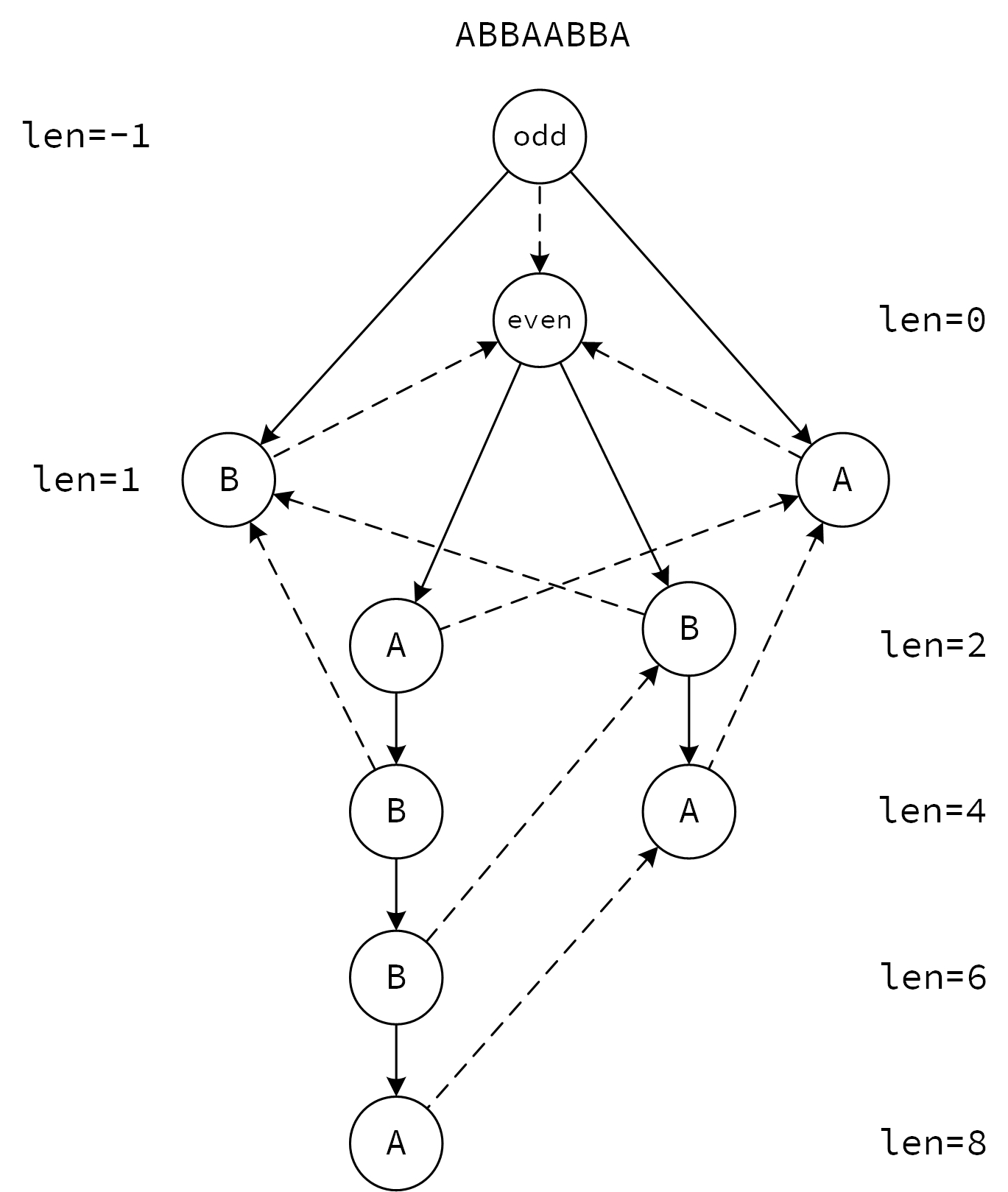
与后缀自动机的一些不同:
- 一个结点只表示一个回文串,这个特性会带来极大的方便。
- 对于 tranc 边来说,奇数和偶数都是树的形式。
- 多了一个 num 表示状态对应的回文串的后缀中回文串的个数(以 fa 为边的树的深度)。
- tranc 边很可能比 fa 边有用。
与后缀自动机的一些相同:
- fa 指针使 len 减少。
- cnt 的含义和计算方法相同。